Xu hướng phát triển của mật mã phi tập trung
Các thế hệ mật mã hàm mới cho phép người dùng chuyển dịch việc sử dụng mô hình client-sever (nơi người dùng buộc phải đặt niềm tin vào máy chủ dịch vụ sang các mô hình phi tập trung - nơi người dùng có thể bỏ qua hoặc không cần tin cậy vào các máy chủ dịch vụ). Các nghiên cứu mới đây về mật mã hàm cho phép người dùng có thể tham gia tính toán một hàm số bất kỳ dựa trên các giá trị đầu vào dưới dạng mã hóa mà không cần chia sẻ bản rõ của dữ liệu cho bất cứ ai.
Một ví dụ của một mật mã phi tập trung là blockchain. Đó là một mạng lưới phân tán, được sử dụng để tạo ra một số loại tiền điện tử như Bitcoin và Ethereum. Trong blockchain, tất cả các giao dịch được ghi lại trên một danh sách liên kết, mỗi giao dịch được mã hóa và bảo mật bằng một chữ ký số. Tất cả các nút trên mạng lưới đều có bản sao của danh sách giao dịch và một giao dịch mới chỉ được thêm vào danh sách nếu được xác nhận bởi đủ số nút trên mạng.
Hướng tới mật mã phi tập trung là một trong những hướng nghiên cứu mới nhất cho hướng đi của mật mã và an toàn thông tin trong lương lai với nhu cầu về các thế hệ mật mã mới như chứng minh không tiết lộ thông tin (Zero Knowledge Proof - ZKP), chứng minh có thể kiểm chứng ngẫu nhiên (Probabilistically Checkable Proof - PCP), các MPC, các hệ mật đồng cấu đầy đủ (Fully Homomorphic Encryption - FHE).
Lịch sử mật mã MPC
Lịch sử mật mã MPC bắt đầu từ những năm 1980, khi các nhà nghiên cứu đã bắt đầu tìm kiếm phương pháp để thực hiện tính toán đồng thời trên dữ liệu bảo mật giữa nhiều thành viên trong mạng mà không cần chia sẻ dữ liệu gốc của họ. Năm 1987, nhà khoa học mạng Yehuda Lindell đã đề xuất giao thức MPC đầu tiên, trong đó mã hóa và chia sẻ dữ liệu giữa các thành viên để tính toán một giá trị hoặc thực hiện một tác vụ nào đó. Sau đó, các nghiên cứu liên tục được thực hiện để cải thiện và mở rộng giao thức MPC, bao gồm việc tăng tính bảo mật và hiệu suất tính toán.
Một ví dụ nổi tiếng về MPC là bài toán triệu phú của Yao. Hai triệu phú muốn biết ai giàu hơn mà không cần tìm hiểu thông tin về khối tài sản thực tế của nhau. Một cách ngây thơ, họ có thể đơn giản nói sự giàu có của mình cho một bên thứ ba. Sau đó, bên thứ ba so sánh sự giàu có của họ và cho họ biết ai là người giàu hơn. Nhưng sau đó, lựa chọn này là không mong muốn vì bên thứ ba biết được thông tin về sự giàu có của họ.
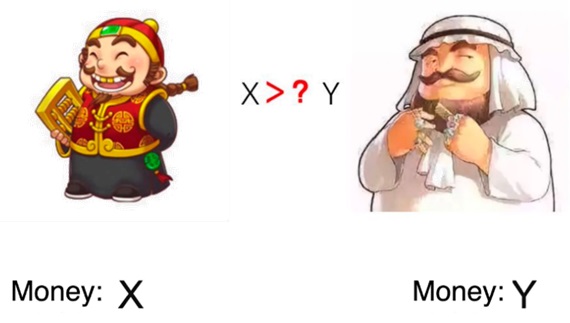
Hình 1. Bài toán triệu phú của Yao.
Thách thức của Bài toán triệu phú của Yao là việc tính toán sẽ không thể có kết quả nếu không có thông tin cá nhân của hai bên. Để có được kết quả cuối cùng, cần những thông tin liên quan đến tính toán. Nhưng đồng thời, không được phép tiết lộ những thông tin cá nhân đó cho bên thực hiện tính toán. Đó là vấn đề chính mà MPC muốn giải quyết.
Thuật toán MPC
Trong giao thức MPC, các bên sẽ thực hiện các bước tính toán trên các dữ liệu riêng tư của mình. Mỗi bên sẽ gửi các phép tính đã được mã hóa đến các bên khác để thực hiện phép tính chung. Sau khi tất cả các bên đã hoàn tất tính toán, kết quả sẽ được trả về cho từng bên. Trong quá trình tính toán, không có bên nào có thể xem dữ liệu của bên khác hoặc kết quả cuối cùng của phép tính.

Hình 2. Minh họa giao thức tính toán bảo mật MPC.
Có nhiều thuật toán được sử dụng trong tính toán bảo mật nhiều thành viên (MPC), bao gồm:
Secure Multi-Party Computation (sMPC): là một phương pháp tính toán bảo mật để tính toán một kết quả chung mà không cần phải chia sẻ dữ liệu cá nhân giữa các thành viên, được xây dựng để bảo mật dữ liệu và tính toán trong môi trường phân tán, nơi các bên không tin tưởng nhau hoàn toàn.
Oblivious Transfer (OT): là giao thức truyền và quên được sử dụng trong MPC, một phương pháp trao đổi dữ liệu mà không cho phép bất kỳ bên nào truy cập hoặc biết về dữ liệu của bên kia, trong đó người gửi chuyển một trong nhiều phần thông tin có khả năng xảy ra cho người nhận, nhưng vẫn không biết về phần nào đã được chuyển. Điều này giúp tăng tính bảo mật cho quá trình trao đổi thông tin giữa hai bên. Hình thức truyền và quên được giới thiệu lần đầu vào năm 1981 bởi Michael O. Rabin. Trong OT, một trong hai bên (người gửi) gửi một số lượng thông tin đến bên kia (người nhận) và cho phép người nhận chọn một trong số các thông tin đó mà họ muốn nhận. Tuy nhiên, người gửi sẽ không biết được thông tin nào đã được chọn bởi người nhận. Còn người nhận sẽ nhận được thông tin mà họ đã chọn nhưng sẽ không biết được thông tin nào còn lại. OT là một trong những thuật toán quan trọng trong MPC vì nó cho phép hai bên trao đổi thông tin mà không cần phải đầu tư vào một bên thứ ba tin cậy để giữ cho quá trình trao đổi an toàn.
Garbled Circuit: là thuật toán được xây dựng trên một mạng lưới tính toán mã hóa, gồm các máy tính được liên kết với nhau. Mỗi máy tính sẽ nhận đầu vào của mình và sau đó sẽ mã hóa dữ liệu theo phương thức bảo mật đã được xây dựng. Sau đó, mỗi máy tính sẽ gửi dữ liệu đã được mã hóa đến một máy tính khác trong mạng lưới. Một khi tất cả dữ liệu đầu vào đã được mã hóa, các máy tính sẽ sử dụng thuật toán Garbled Circuit để tính toán kết quả chung mà không cần phải chia sẻ bất kỳ thông tin nào về dữ liệu đầu vào. Kết quả cuối cùng sẽ được giải mã và chia sẻ cho tất cả các thành viên trong mạng.
Homomorphic Encryption (HE): là một kỹ thuật mã hóa cho phép tính toán trên dữ liệu được mã hóa mà không cần giải mã dữ liệu đó. HE cung cấp một cách bảo mật cho dữ liệu riêng tư và cho phép các tính toán được thực hiện trên dữ liệu mà không cần phải giải mã dữ liệu. Điều này cung cấp một cách bảo mật tốt hơn cho các ứng dụng mã hóa như dịch vụ chuyển tiền trực tuyến, bảo mật dữ liệu trên đám mây và các dịch vụ cho phép tính toán trên dữ liệu mã hóa. HE còn cung cấp một cách bảo mật cho các tính toán phức tạp, như các tính toán trên dữ liệu tối mật và các tính toán trên dữ liệu của nhiều người dùng khác nhau.
Việc chọn thuật toán mã hóa MPC phù hợp sẽ phụ thuộc vào nhu cầu bảo mật và hiệu suất tính toán của mỗi ứng dụng cụ thể. Chính vì thế, các nghiên cứu liên tục được thực hiện để phát triển và cải thiện thuật toán mã hóa MPC. Một số ưu điểm của MPC bao gồm:
Chia sẻ tin cậy: trong tính toán nhiều bên an toàn, dữ liệu có thể được chia sẻ theo cách phân tán với các tổ chức khác nhau mà không cần bất kỳ bên thứ ba nào và thậm chí quyền riêng tư của dữ liệu sẽ được bảo toàn trong khi chia sẻ dữ liệu.
Bảo mật dữ liệu: dữ liệu riêng tư của các tổ chức có thể được chia sẻ cho mục đích tính toán. Mối quan tâm về quyền riêng tư của dữ liệu được cung cấp bằng cách sử dụng tính toán đa bên an toàn, giúp cho dữ liệu được sử dụng ở dạng mã hóa. Do đó, dữ liệu không bị tiết lộ hoặc bị xâm phạm.
Độ chính xác cao: tính toán nhiều bên an toàn cung cấp kết quả có độ chính xác cao cho các phép tính khác nhau bằng mật mã.
An toàn trước các cuộc tấn công: dữ liệu được chia sẻ giữa các bên an toàn trước các cuộc tấn công với mục đích xấu vì dữ liệu được chia nhỏ và mã hóa khi được phân phối giữa các bên để tính toán.
Tính toán MPC đang được sử dụng để giải quyết các vấn đề khác nhau, nhưng có một số hạn chế. Để cung cấp tính năng bảo mật, dữ liệu cần được mã hóa và sinh ngẫu nhiên, việc sinh ngẫu nhiên có thể yêu cầu nhiều chi phí tính toán hơn, điều này làm chậm thời gian xử lý thuật toán. Việc phân phối dữ liệu cho nhiều bên để tính toán qua mạng dẫn đến chi phí vận hành cao hơn.
Các giao thức MPC có thể được sử dụng trong nhiều ứng dụng khác nhau, bao gồm bầu cử điện tử, phân tích dữ liệu bảo mật, học máy an toàn và nhiều hơn nữa. Tuy nhiên, chúng có thể yêu cầu sự tính toán phức tạp và khó triển khai. Các nhà nghiên cứu đang phát triển các giao thức MPC để cải thiện hiệu quả và tăng khả năng ứng dụng của chúng. Các mô hình mật mã mới này hứa hẹn sẽ là một hướng nghiên cứu chủ đạo về mật mã trong tương lai gần khi người dùng cần hơn quyền tự do, riêng tư và sở hữu dữ liệu của chính bản thân mình. Các mô hình mật mã sẽ đóng vai trò lớn trong việc tạo ra thuật toán học máy an toàn giúp con người có thể kiểm soát được những tác động của học máy mà chưa lường trước được.
TÀI LIỆU THAM KHẢO
1. https://en.wikipedia.org/wiki/Yao%27s_Millionaires%27_problem.
2. A.C. Yao (1982), Protocols for secure computations, 23rd annual symposium on foundations of computer science (sfcs 1982).
3. M. Daiki, et al. (2020), "Practical card-based implementations of Yao's millionaire protocol", Theoretical Computer Science, 803, pp.207-221.
4. M.O. Rabin (2005), How to exchange secrets with oblivious transfer, Cryptology ePrint Archive.